42 Push Swap Report 📘

(Updated: )
dev › 42project
, , , , , ,

Project Overview: Push Swap 42 School Project

Introduction

Push Swap is a project assigned within the curriculum of 42 School, designed to challenge students’ understanding of sorting algorithms and their ability to optimize code for efficiency. The project involves sorting a stack of integers using a limited set of operations, with the goal of arranging the numbers in ascending order on a separate stack. While there are various sorting algorithms available, students are encouraged to explore and implement different approaches to achieve optimal sorting performance.

Project Description

The Push Swap project requires students to implement a sorting algorithm to arrange a stack of integers in ascending order using a limited set of operations, which include swapping, rotating, and pushing elements between two stacks. The primary objective is to develop an efficient sorting algorithm with minimal complexity, utilizing the provided operations to manipulate the stacks and achieve the desired sorting outcome. Additionally, one of the goals of the project is to minimize the maximum number of cycle operations required for sorting, without focusing on memory efficiency or performance optimization.

Sorting Algorithms

While there are multiple sorting algorithms to choose from, students often explore various options to determine the most suitable approach for the Push Swap project. Some common sorting algorithms include:

  • Radix Sort: Utilized for its simplicity and efficiency, particularly when dealing with integers.
  • Papillon Sort: A mixed algorithm combining elements of quicksort and insertion sort, known for its adaptability to different datasets.
  • Quicksort: A popular divide-and-conquer sorting algorithm, characterized by its efficiency and effectiveness on average.
  • Custom Sort Algorithms: Some students opt to develop custom sorting algorithms tailored to the specific requirements and constraints of the Push Swap project.

Approach

In approaching the Push Swap project, students are encouraged to analyze the characteristics of different sorting algorithms and evaluate their performance under various scenarios. Factors such as time complexity, space complexity, and the number of required operations play a crucial role in determining the optimal approach. Additionally, students may explore optimization techniques to enhance the efficiency and speed of their sorting algorithm.

Personal Opinion

My opinion of this project is very positive. I like projects like Push Swap because they are very technical and involve a deep understanding of sorting algorithms. Sorting algorithms fascinate me; understanding how they work, comparing them and optimizing program execution is incredibly rewarding. I highly recommend taking the time to work on this project and delving deeper into sorting algorithms. Today, many programming companies require rote knowledge of at least three sorting algorithms, making this project invaluable to your skill set. Unfortunately for me at the time, I was still in the core curriculum, so I didn’t take the time to delve too deeply, but I encourage you to do it again later, or to train yourself in sorting algorithms on platforms such as coding game, or by coding yourself a library that implements sorting algorithms, then compare their performance with library such as libcriterion to test your algorithms in a unitary way, then benchmark to measure performance and algorithms complexity.

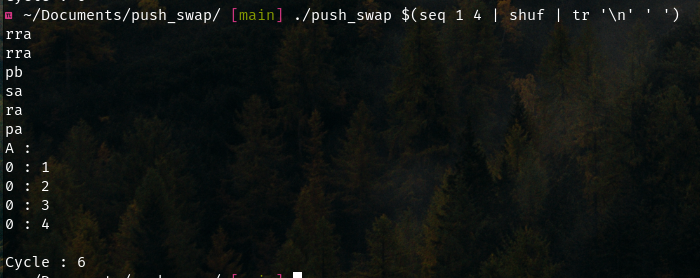
Screenshot

Screenshot

Big (O) Notation measure algorithms complexity

AC

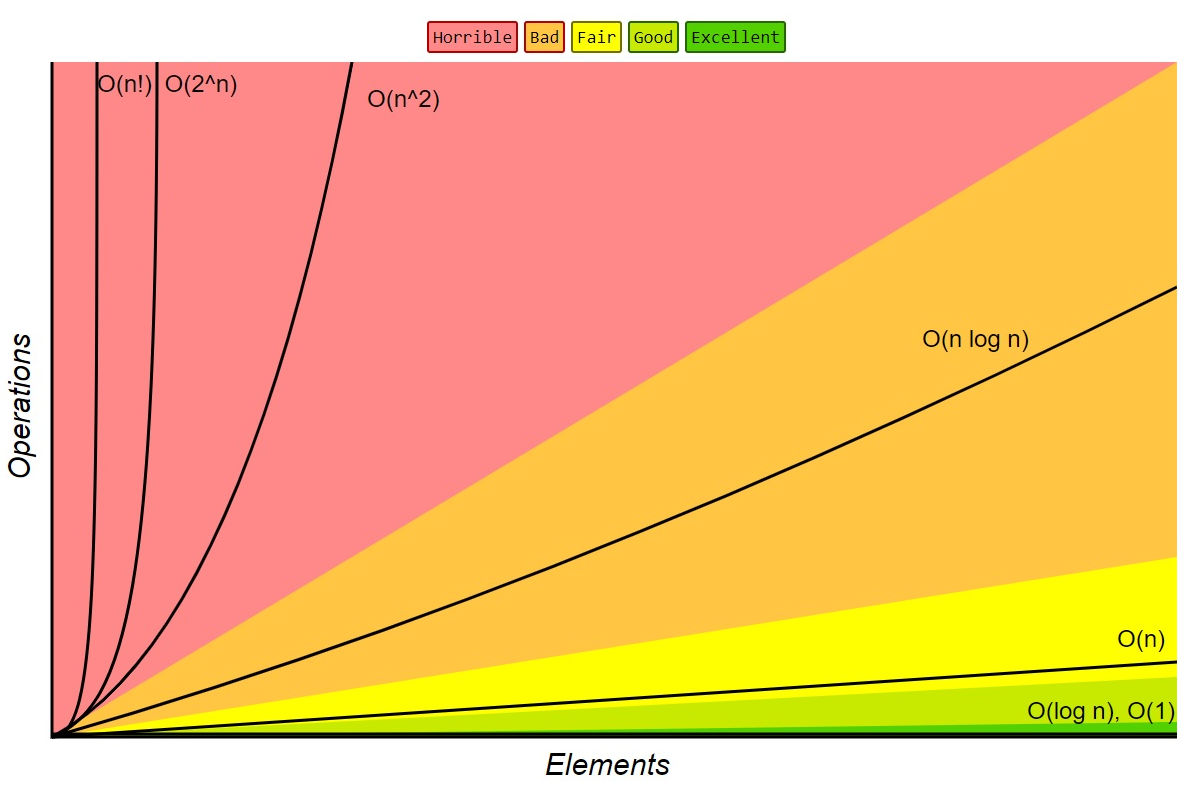
Notation Quality Description Example
O(1) Excelent This notation describes algorithms with constant time complexity, meaning that their runtime does not depend on the size of the input. Regardless of how large the input is, the algorithm will execute in a constant amount of time. An example of an O(1) operation is accessing an element in an array by index. An example of O(1) complexity where M is used could be accessing an element in a matrix (M) by its row and column indices.
O(log n) Good Logarithmic time complexity means that the runtime of the algorithm grows logarithmically as the size of the input increases. Algorithms with O(log n) complexity often involve dividing the input in half at each step, such as binary search on a sorted array. This is much faster than linear time complexity but slower than constant time complexity. complexity where n is used could be binary search in a sorted array.
O(n) Fair Linear time complexity indicates that the runtime of the algorithm grows linearly with the size of the input. In other words, if the input size doubles, the runtime will also approximately double. Common examples of O(n) algorithms include iterating through an array or a linked list. O(n) complexity could be finding the maximum element in an unsorted array.
O(n log n) Bad This notation describes algorithms with a runtime that grows in proportion to n times the logarithm of n. Algorithms with O(n log n) complexity are often seen in efficient sorting algorithms like merge sort and quicksort. They are faster than quadratic time complexity but slower than linear and logarithmic time complexity. O(n log n) complexity could be sorting an array using an efficient comparison-based sorting algorithm like merge sort.
O(n^2) Horrible Quadratic time complexity indicates that the runtime of the algorithm grows quadratically with the size of the input. This means that if the input size doubles, the runtime will approximately quadruple. Examples of algorithms with O(n^2) complexity include nested loops where each loop iterates over the entire input. O(n^2) complexity could be the bubble sort algorithm, which repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order.
O(2^n) Horrible Exponential time complexity describes algorithms whose runtime doubles with each additional element in the input. This type of complexity is generally considered inefficient and can quickly become unmanageable for larger inputs. An example of an algorithm with O(2^n) complexity is the recursive solution to the Tower of Hanoi problem. O(2^n) complexity could be the recursive solution to the “power set” problem, which involves generating all possible subsets of a set.
O(n!) Horrible complexity means the runtime of an algorithm grows factorially with the size of the input (denoted by n). This growth rate is extremely rapid and impractical for all but the smallest inputs. It’s mainly encountered in algorithms that generate permutations or combinations of elements, where every possible arrangement must be considered. Due to its inefficiency, other approaches are preferred for larger inputs. O(n!) complexity could be a naive recursive solution to generating permutations of a set

You can also see the Algorithm Complexity in resources.

Conclusion

The Push Swap project challenges students to apply their knowledge of sorting algorithms and optimization techniques to efficiently sort a stack of integers using a limited set of operations. By exploring different sorting algorithms and analyzing their performance characteristics, students gain valuable insights into algorithmic complexity and problem-solving strategies. Furthermore, the project encourages experimentation and creativity in developing custom solutions tailored to specific requirements and constraints.

🔍 Let the sorting adventure begin! 📊

Sources:

Subject

Download the subject just here